連関資料 :: 実験
資料:324件
全体公開 2022/07/14
-
体液のホメオスタシスに関する実験
- 目的：水・電解質・重曹を負荷した後に尿を採取してpH・浸透圧等を測定することで、体液のホメオスタシスについて理解する。またpHの緩衝作用について学習することで、生体の酸塩基平衡について理解する。 ?：体液のホメオスタシスに関する実験 器具・材料：１、水700(ml)、0.9%食塩水700(ml)、1.5%重曹水700(ml)、0.5Mスクロース、0.5MNaCl ２、pH試験紙、浸透圧計 ＜実験１＞＝浸透圧と濃度＝ グラフ入り 方法：0.5Mスクロースと0.5MNaClをそれぞれ50(ml)とり、濃度が半分になるように希釈した。この操作を３回繰り返し、作成したそれぞれの濃度の溶液の浸透圧を記録した。 結果：上の表・グラフに示すような結果が得られた。 考察：浸透圧は濃度が高い程高くなる為、濃度を半分にしていけば、浸透圧もほぼ半分になると考えられる。またNaClは非常に強い電解質であり、溶液中ではほとんどが Na+とCl-の２分子として存在している。スクロースは１分子で存在している為、浸透圧はNaClの方が比較的高くなる。 ＜実験２＞＝水の再吸収＝ グラフ入りー
- レポート 医・薬学 ホメオスタシス 酸 塩基 ヘンダーソン クリアランス
550 販売中 2006/03/18- 閲覧(4,059)
-
酵素科学実験
- 酵素科学実験（タンパク質の精製・酵素学実験） 【実験目的】 酵素の精製法及び活性の測定方法を身につける。 酵素活性の単位について理解する。 【実験方法】 実験Ⅰ 酵素活性の測定 ＜使用試薬＞ 0.5M Tris-HCl Buffer (pH8.5) ，L-カルニチン溶液 (50mM) 発色剤 ，酵素液 ，NAD溶液(5mM) ，0.5N HCl ＜操作＞ ・・・ 実験Ⅱ 反応時間と基質変化量の関係 ＜使用試薬＞ 0.5M Tris-HCl Buffer (pH8.5) ，L-カルニチン溶液 (50mM) 発色剤 ，酵素液(A＝×3200 B=×800) ，NAD溶液(5mM) ，0.5N HCl ＜操作＞ 実験Ⅲ イオン交換クロマトグラフィー ＜使用試薬＞ 陰イオン交換樹脂（DEAE-トヨパール） 平衡化用Buffer（10mM リン酸カリウムBuffer pH7.5 ＋ 2-メルカプトエタノール） 溶出用Buffer(0.2M KCl , 0.4MKCl) 酵素粗抽出液 , 0.5M Tris-HCl Buffer (pH8.5) ，L-カルニチ
- 酵素 精製 酵素活性 unit PAGE イオン交換クロマトグラフィー
- 550 販売中 2008/08/03
- 閲覧(3,954)
-
微生物実験
- 今実験では、カビ（A.oryzae NBRC 30113）、酵母（S.cerevisiae NBRC 0304）、枯草菌（B.subtilis NBRC 3009）、大腸菌（E.coli NBRC 3301）の4つの菌を、自作の倍地に植菌、培養し、肉眼観察、顕微鏡による観察、菌数計算板による生菌数の測定、グラム染色を行い、得られた結果から、菌の持つ性質を調査し、菌を分類した。 序論 ●微生物とは 実験方法 ●綿栓の作成 ●培地の作成 ●微生物の植菌 ●微生物の培養 観察・結果 ●カビの観察 ●酵母の観察 ●枯草菌、大腸菌の観察 ] ●グラム染色 考察 ●カビの観察について ●酵母の観察について ●菌数計算板による全菌数の測定 ●枯草菌の観察について ●大腸菌の観察について 参考文献
- 酵母 大腸菌 微生物実験 カビ 枯草菌 グラム染色
- 550 販売中 2010/04/16
- 閲覧(7,391)
-
マイクロスリップの実験
- マイクロスリップの実験 １．目的 人々は日常の生活の中で、様々な行為を行っている。コーヒーを入れる作業や食事中の手の動きを注意深く観察してみると、対象を掴もうと伸ばした手の動きが、あたかも躊躇したかのように微小に停滞したり、ある対象に向かう手の軌道が途中で別の対象に向かう軌道へと急速に変化したり、ある対象にわずかに接触した後に別の対象に向かうといった微小な行為の修正が頻繁に起こっていることに気づく。このような、いったん開始したにもかかわらず途中で修正されてしまう微小なスリップ様の現象は、マイクロスリップと呼ばれている（Reed，1992；鈴木，2001）。マイクロスリップは、私たちの日常生活での行為について検討する上で非常に興味深い現象である。本実験は、マイクロスリップの起こり方と環境の複雑さとの関連について調べることを目的とする。 ２．方法 被験者：単純条件 14名（男4女10）平均19.8才 複雑条件 14名（男5女9）平均19.1才 器具：単純条件では、テーブルに縦4列横3列の枠を書いた紙を敷き、枠内には空の紙コップ2個と砂糖の入ったもの、クリーム粉の入った
- 実験 分析 課題 方法 理解 記録 生活 目的 時間 コーヒー
- 550 販売中 2008/08/13
- 閲覧(3,495)
-
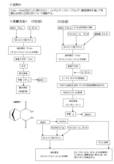
実験（Diels-Alder）
- Diels－Alder反応により得られる2－ノルボルネン-5,6－ジカルボン酸誘導体を通して有機化合物の立体化学について理解する。 ＜実験方法＞ （1日目） ＜目的＞ 試料１ 3.8 g 水 50 ml 100 ml ナス型フラスコ 試料2へ 融点測定 （素焼き板） 加熱還流 15 min （オイルバス＆リービッヒ冷却管） 室温で冷却 1 hour 氷冷 吸引濾過 秤量 2.81 g 0.34 gを38班から補う NaHCO3飽和水溶液 10 mlで2回有機層を洗浄する エーテル 20 mlで2回抽出 MgSO4 3.01 gで乾燥 減圧蒸留 （エバポレーター） （２日目） 試料2 2.94
- 有機実験 ディールスアルダー TLC 実験手順 東工大
- 550 販売中 2008/04/18
- 閲覧(4,038)
